Clustering

Clustering

• Broad set of techniques for finding subgroups.
• Observations within groups are quite similar to each other and observations in different groups quite different from each other.

Clustering methods

• Partitioning: k-means clustering
• Agglomerative/divisive: hierarchical clustering
• Model-based: mixture models

K-means clustering

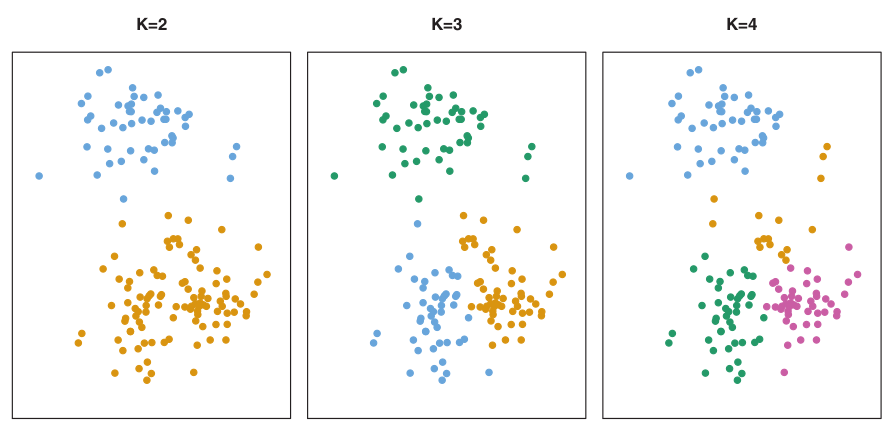
• Simple approach to partitioning a data set into K distinct, non-overlapping clusters.
• K is specified beforehand.

James et al. 2013

K-means algorithm

• \(K\) – number of clusters.

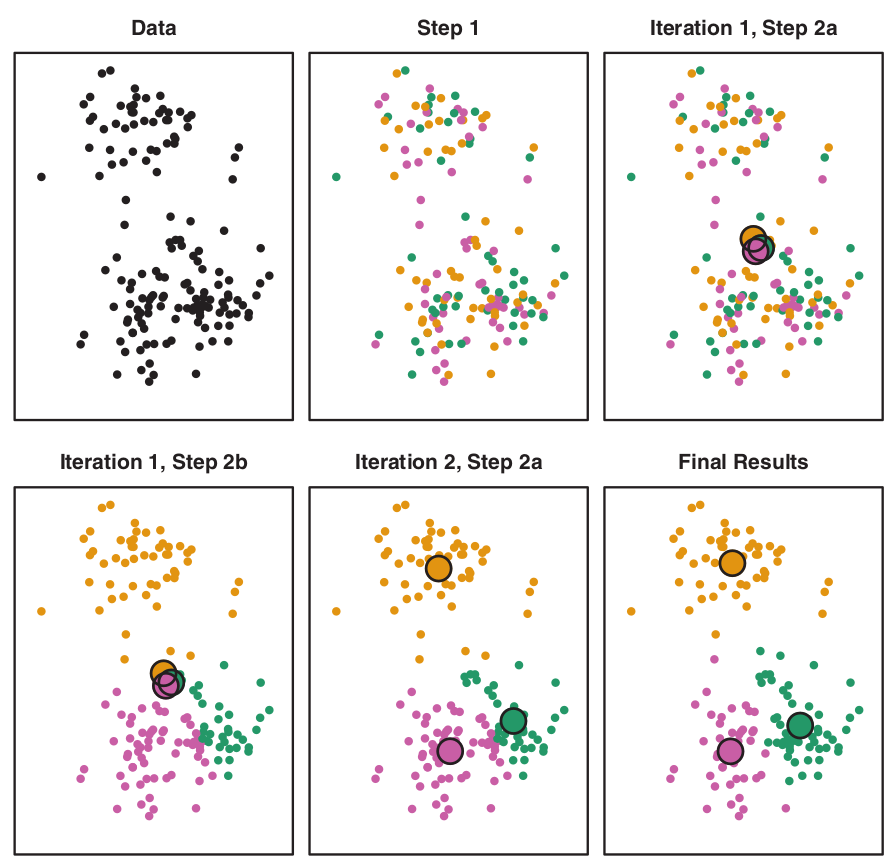
The process:

1. Randomly assign each observation to groups 1 to K;
2. For each of K clusters, derive its centroid (midpoint);
3. Reassign each observation into a cluster whose centroid is the closest;
4. Iterate until stability in cluster assignments is reached (local vs global optima).

James et al. 2013

Some properties of K-means partitioning

• Standard algorithm for k-means clustering is using Euclidean distance (distances are calculated using Pythagorean theorem).
• Different local optima (stability) can be reached.

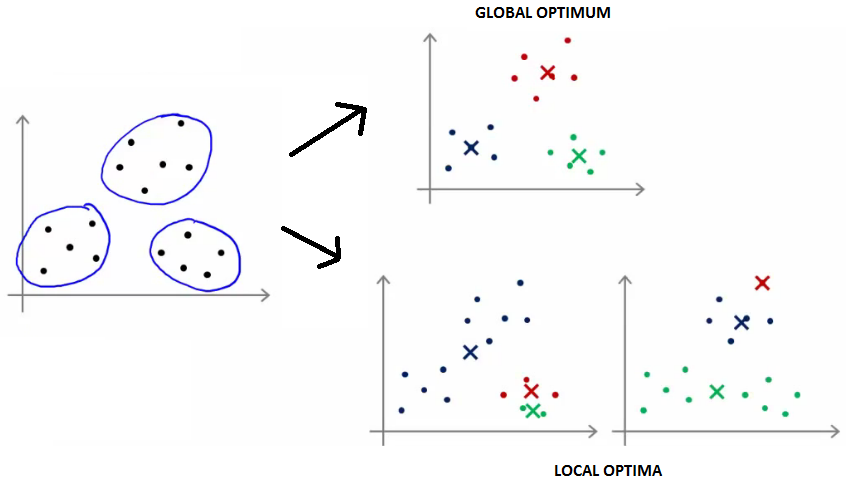
• Number of clusters K must be specified in advance

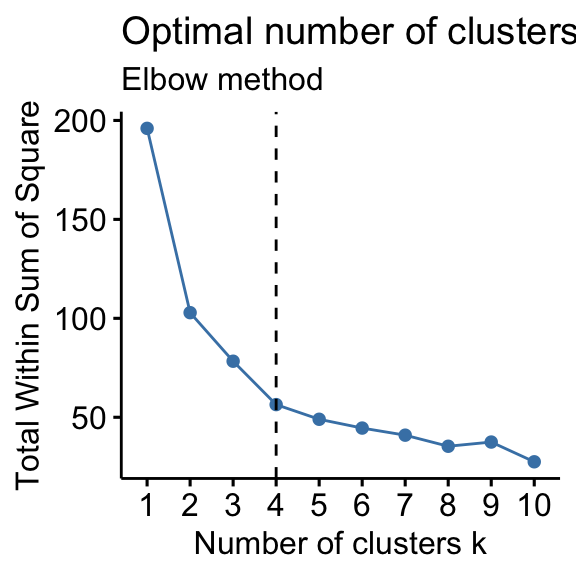
• How to determine optimal number of clusters?

  • Elbow method,
  • Silhouette method

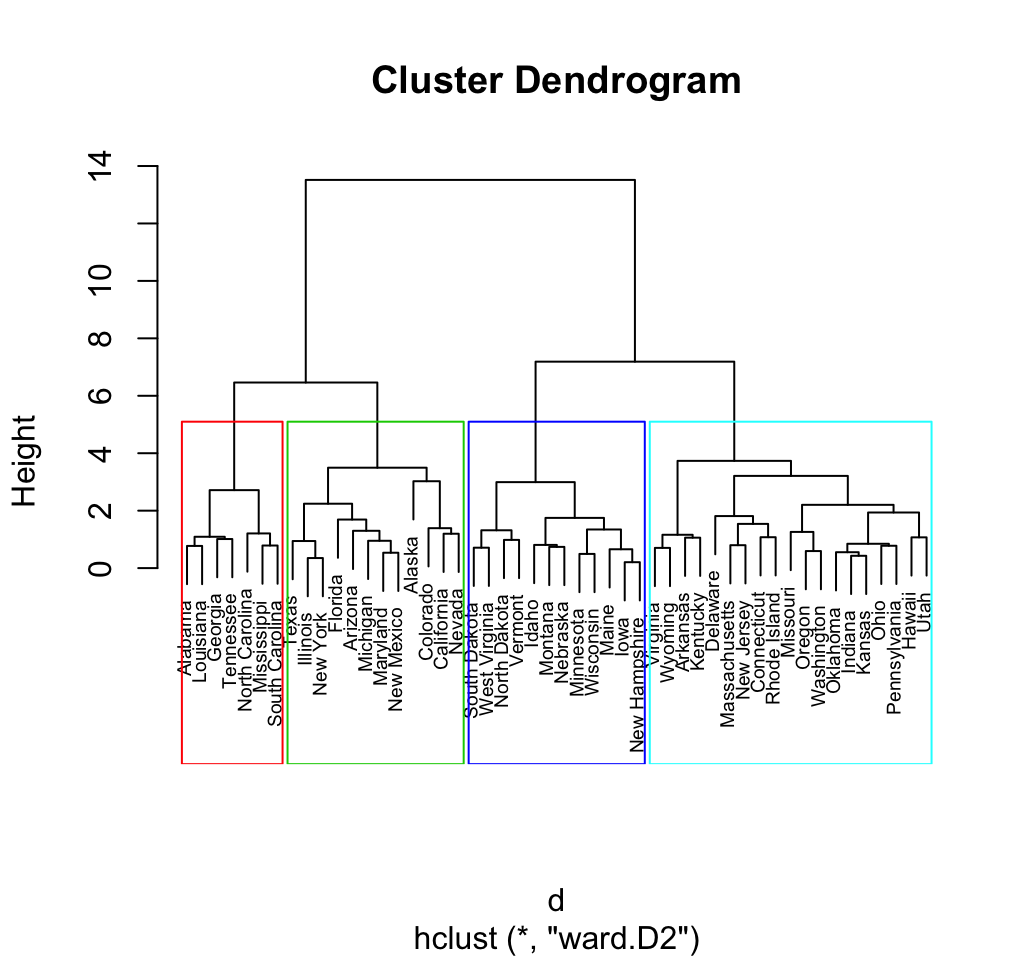
Hierarchical clustering

• The number of clusters is not specified beforehand.
• Output is a dendrogram – a hierarchical structure visualizing the cluster growth.
• Starts with a distance matrix.

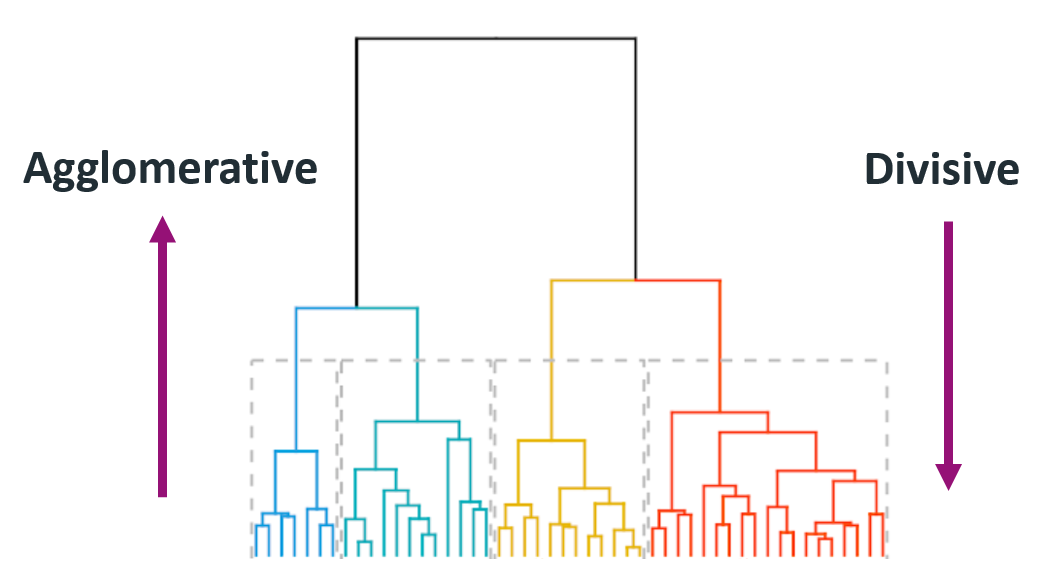
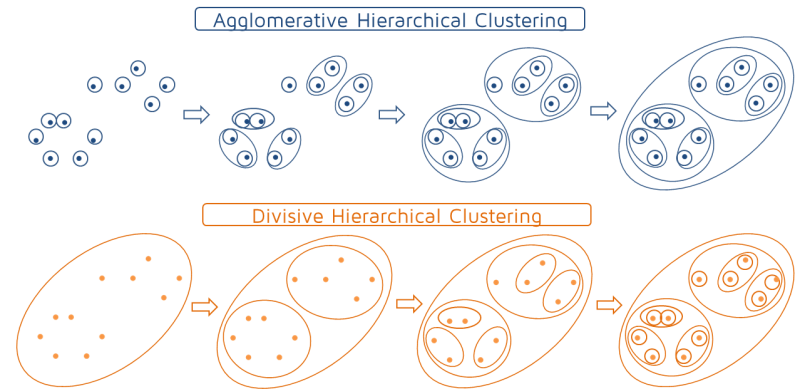
Agglomerative

• Builds the hierarchy of clusters from bottom-up until a single cluster is reached.

1. Put each object in its own cluster;
2. Join the clusters that are the closest;
3. Iterate until a single cluster encompassing all objects is reached.

Divisive

• Divides a single large cluster into individual objects (top-down).

1. Put all objects into a single cluster;
2. Divide the cluster into subclusters at a similar distance;
3. Iterate util all objects are in their own clusters.

Hierarchical clustering algorithms

Clustering methods comparison

K-means partitioning

• Pre-specified number of clusters.
• Clusters may vary (different local optima).
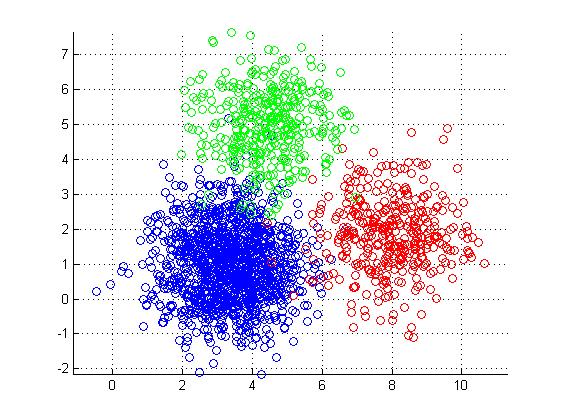
• Best when groups in data are (hyper)spheres.

Hierarchical clustering

• Variable cluster numbers.
• Clusters are stable.
• Any shape of data distribution.