Distances and similarity

Distance and similarity are more or less opposite concepts.
Distance is a numerical measure describing how are two objects (defined by certain variables) different (pairwise distance).
Different distance measures exist for different data types.

Distance

Scale 0 – \(\infty\)
0 – Two objects with 0 distance between them.
\(\infty\) – Two objects with infinite distance.
In practice, maximum distance is often 1.
Denoted by \(D\) (for distance, or dissimilarity).
\(D = 1 - S\)

Similarity

Scale 0 – 1
0 – Two objects completely dissimilar (0%).
1 – Two objects competely similar (100%).
Denoted by \(S\) (for similarity).
\(S = 1 - D\)

Different distance measures

Dichotomous variables
- Symmetrical – Simple matching distance
- Asymmetrical – Jaccard index (binary distance)
Categorical variables
- Hamming distance
Numeric continuous variables
- Euclidean distance
- Mahalanobis distance
Mixed data sets
- Gower’s distance

Binary distances

For TRUE/FALSE, 1/0, presence/absence (etc.) data

Symmetrical

Two presences as match.
Two absences as match.

If a trait is present, two objects are more similar. If a trait is absent, two objects are more similar. For example if biological sex is encoded in one variable with 0 for male and 1 for female, it is symmetrical.

Simple maching distance

Asymmetrical

Two presences as match.
Two absences as mismatch.

If a trait is present, two objects are more similar. If a trait is absent in both cases, e.g. undetermined, missing etc., this does not affect similarity. This is more practical in archaeology.

Jaccard index, i.e. binary distance

dist(x, method = "binary")

Distance between (continuous) numeric data

To remove effects of scale (different units etc.), variables should be scaled (normalized).

Normalization

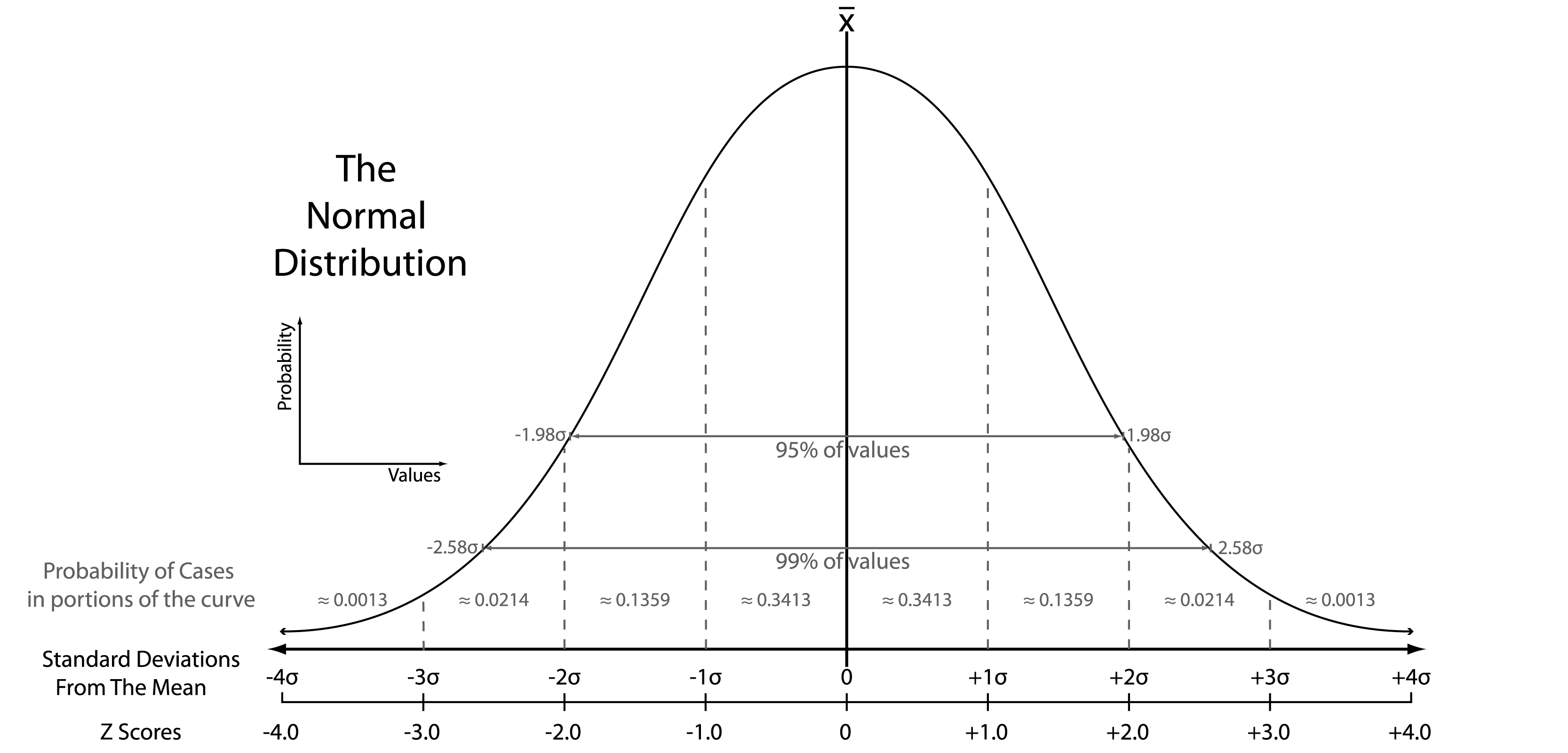
z-score or z-transformation

\[ z = \frac{x - \mu}{\sigma} \]

Euclidean distance

Defined for a Cartesian coordinate space.
Uses Pythagorean theorem.

\[ d(p, q) = \sqrt{(q_1 - p_1)^2 + (q_2 - p_2)^2} \]

In R…

Normalization:
scale(x, center = TRUE, scale = TRUE)

Euclidean distance:
dist(x, method = "euclidean")

Code along

library(dplyr)
darts <- read.csv("https://petrpajdla.github.io/stat4arch/lect/w09/data/dartpoints_numeric.csv")

# summary of values
summary(select(darts, Length, Width, Thickness, Weight))

     Length           Width         Thickness          Weight      
 Min.   : 30.60   Min.   :14.50   Min.   : 4.000   Min.   : 2.300  
 1st Qu.: 40.85   1st Qu.:18.55   1st Qu.: 6.250   1st Qu.: 4.550  
 Median : 47.10   Median :21.10   Median : 7.200   Median : 6.800  
 Mean   : 49.33   Mean   :22.08   Mean   : 7.271   Mean   : 7.643  
 3rd Qu.: 55.80   3rd Qu.:25.15   3rd Qu.: 8.250   3rd Qu.:10.050  
 Max.   :109.50   Max.   :49.30   Max.   :10.700   Max.   :28.800

# normalization
darts_norm <- darts %>%
  mutate(Length = scale(Length), Width = scale(Width),
         Thickness = scale(Thickness), Weight = scale(Weight))
         
# or this shorthand can be used
darts_norm <- darts %>%
  mutate(across(all_of(c("Length", "Width", "Thickness", "Weight")), scale))

# summary of normalized values
summary(select(darts_norm, Length, Width, Thickness, Weight))

         Length.V1                 Width.V1                 Thickness.V1       
 Min.   :-1.470672596590   Min.   :-1.469439528820   Min.   :-2.1363402766800  
 1st Qu.:-0.665879481618   1st Qu.:-0.683997993872   1st Qu.:-0.6670232741610  
 Median :-0.175151972489   Median :-0.189460731127   Median :-0.0466449842071  
 Mean   : 0.000000000000   Mean   : 0.000000000000   Mean   : 0.0000000000000  
 3rd Qu.: 0.507940720219   3rd Qu.: 0.595980803820   3rd Qu.: 0.6390362836370  
 Max.   : 4.724271478660   Max.   : 5.279539586280   Max.   : 2.2389592419400  
         Weight.V1        
 Min.   :-1.269965702070  
 1st Qu.:-0.735153942506  
 Median :-0.200342182946  
 Mean   : 0.000000000000  
 3rd Qu.: 0.572163691974  
 Max.   : 5.028928354970

Code along

# subset of Travis and Darl types of dart points
darts_subset <- filter(darts_norm, Name %in% c("Travis", "Darl")) 

# matrix with numerical variables only
darts_mx <- darts_subset %>% 
  select(Length, Width, Thickness, Weight) %>% 
  as.matrix()
  
# add row names to the matrix
rownames(darts_mx) <- darts_subset$Name

# count Euclidean distance 
darts_d <- dist(darts_mx, method = "euclidean", diag = TRUE)

round(as.matrix(darts_d)[1:6, 1:6], 2)

     Darl Darl Darl Darl Darl Darl
Darl 0.00 0.42 0.47 0.40 1.57 1.14
Darl 0.42 0.00 0.43 0.43 1.50 1.18
Darl 0.47 0.43 0.00 0.28 1.51 1.36
Darl 0.40 0.43 0.28 0.00 1.74 1.47
Darl 1.57 1.50 1.51 1.74 0.00 0.90
Darl 1.14 1.18 1.36 1.47 0.90 0.00

Result is a distance matrix.
It is symmetrical. Lower triangular is the same as upper triangular.
On the diagonal, there is distance of the given object to itself, i.e. 0.

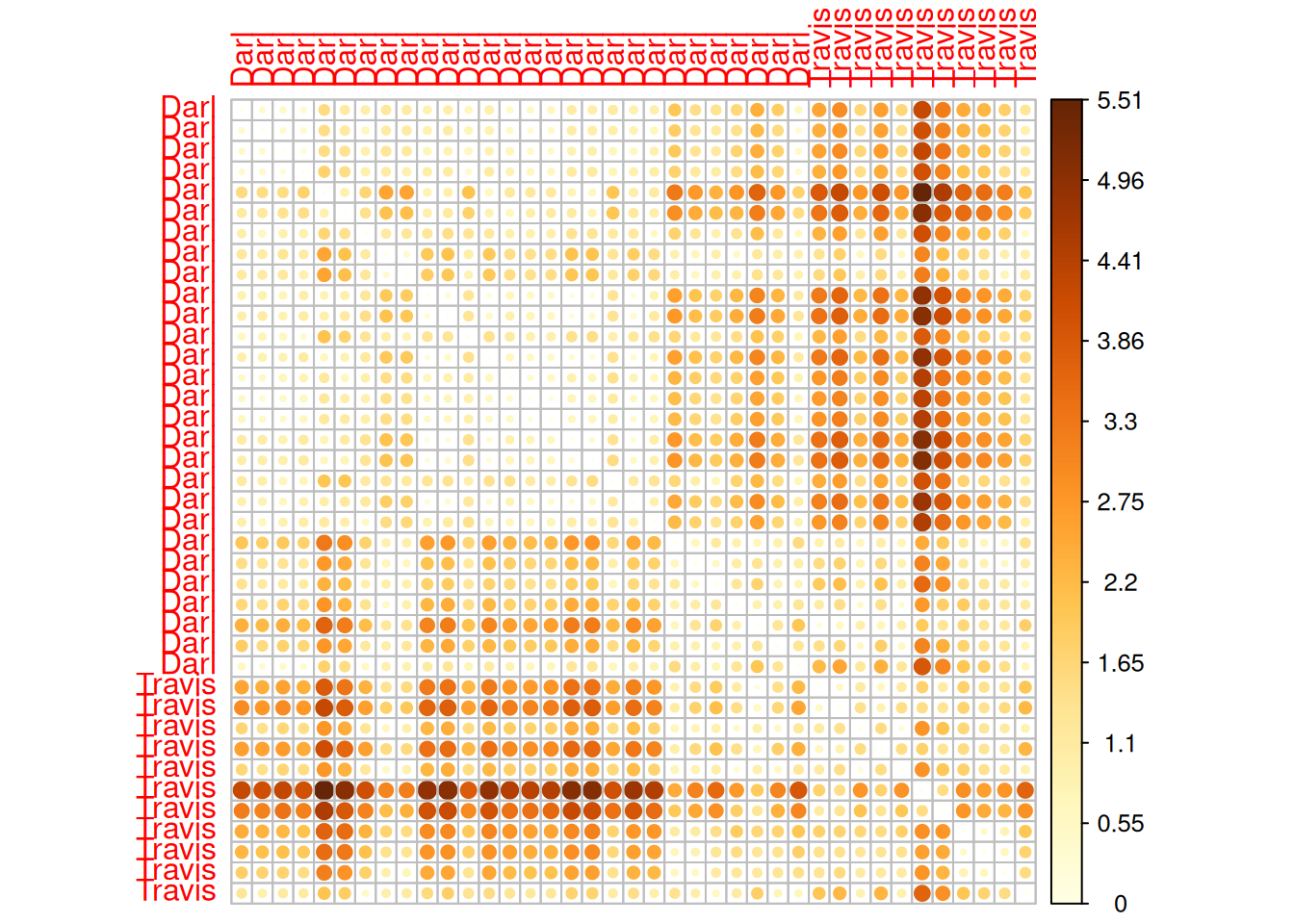
Visualizing distance matrix

Package corrplot has a nice way of plotting heatmaps.

library(corrplot)

# arg. is.corr set to FALSE, because we are not visualizing correlation matrix
corrplot(as.matrix(darts_d), is.corr = FALSE)

Resources

For a much more detailed overview of distance methods, see the tutorial on classification by Schmidt, S. C. et al. DOI: 10.5281/zenodo.6325372 (direct link to a HTML file is here).